Albero AVL
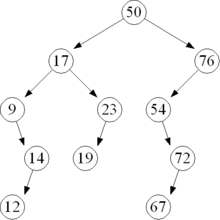
L'albero AVL è, in informatica, un albero binario di ricerca bilanciato in cui il coefficiente di bilanciamento per ciascun nodo vale 1, 0 oppure -1 (nel caso di un albero AVL completo tutti i coefficienti di bilanciamento sono uguali a 0).

Il nome AVL viene dai suoi inventori Adelson-Velskij e Landis, che pubblicarono il loro algoritmo nel saggio in russo "Odin algoritm organizacii informacii" ("un algoritmo di organizzazione dell'informazione") del 1962.
Viene definito il coefficiente di bilanciamento come la differenza tra le altezze, rispettivamente, del sottoalbero sinistro e del sottoalbero destro di un nodo:
dove è il nodo di cui si vuole calcolare il coefficiente e e sono rispettivamente il figlio sinistro e il figlio destro di .
può quindi assumere solo valori interi sia positivi che negativi.
La condizione per tenere l'albero bilanciato è semplice: per ogni nodo dell'albero, la differenza di altezza dei suoi sottoalberi figli deve differire al massimo di uno ( ). Grazie a questa restrizione, l'altezza massima dell'albero, ossia la più grande distanza tra la radice e le foglie, è logaritmica nel numero dei nodi. È per questo che questa struttura di dati permette di compiere l'inserimento, la ricerca e l'eliminazione di un elemento in O(log n). Inoltre se si considerano i costi ammortizzati di una serie di inserzioni, questi sono O(1).
Per evitare di dover contare ogni volta l'altezza di un sottoalbero, si salva nel nodo il coefficiente di bilanciamento di un nodo, che è definito come la differenza tra l'altezza del sottoalbero sinistro e quella del sottoalbero destro del nodo considerato.
Rotazioni
modificaUn nodo con il coefficiente di bilanciamento diverso da 1, 0 o -1 è considerato sbilanciato e viene ribilanciato grazie alle rotazioni. Ne esistono tre tipi:
Rotazione a sinistra
modificaSi esegue quando un nodo ha un coefficiente di bilanciamento di -2 ed il suo figlio destro un coefficiente di bilanciamento uguale a -1.
Rotazione a destra
modificaSi esegue quando un nodo ha un coefficiente di bilanciamento di +2 e il suo figlio sinistro un coefficiente di bilanciamento uguale a +1.
Doppia rotazione
modificaSinistra-Destra
modificaSi esegue quando un nodo ha un coefficiente di bilanciamento di +2 e il suo figlio sinistro un coefficiente di bilanciamento uguale a -1.
Destra-Sinistra
modificaSi esegue quando un nodo ha un coefficiente di bilanciamento di -2 e il suo figlio destro un coefficiente di bilanciamento uguale a +1
Operazioni
modificaRicerca
modificaLa ricerca di un elemento in un albero AVL si svolge come quella negli alberi binari di ricerca.
Inserimento
modificaIl primo passo dell'inserimento di un elemento in un albero AVL funziona come in quello non bilanciato, si cerca il posto dove deve andare. Se la ricerca finisce su un nodo contenente l'elemento da inserire, l'inserimento è terminato, mentre se finisce in una foglia, la si sostituisce con un nodo contenente l'elemento da inserire. Dopo questa operazione, il giusto bilanciamento dell'albero non è più garantito. L'algoritmo quindi aggiorna i coefficienti di bilanciamento e controlla se sul percorso dal nuovo nodo alla radice ci siano nodi dove la condizione di bilanciamento non è soddisfatta. In questo caso viene applicata una serie di rotazioni che ripristina tale invariante.
Eliminazione
modificaAnche qui, si cerca l'elemento da eliminare come negli alberi binari di ricerca. Se l'elemento non è presente, non bisogna fare niente. Se è una foglia o ha un solo figlio, il nodo viene rimosso e l'eventuale unico figlio agganciato al padre del nodo rimosso; altrimenti si sostituisce il nodo con una foglia che ne costituisce il suo diretto predecessore o successore[1]. A questo punto le condizioni di bilanciamento non sono più garantite sul percorso che va dalla radice al nodo rimosso fino eventualmente alla foglia che lo ha sostituito; l'algoritmo quindi procede ripristinando il bilanciamento su questi nodi tramite una serie di rotazioni.
Note
modifica- ^ La scelta dell'uno o dell'altro è indifferente.
Bibliografia
modifica- G. Adelson-Velskii and E.M. Landis, "Odin algoritm organizacii informacii" Doklady Akademii Nauk SSSR, 146:263–266, 1962 (russo)
Voci correlate
modificaAltri progetti
modifica- Wikimedia Commons contiene immagini o altri file sull'albero AVL
Collegamenti esterni
modifica- Paul E. Black, AVL tree, in Dictionary of Algorithms and Data Structures.





