Collider (statistica)
In statistica e nel contesto dei grafi causali, una variabile è un collider quando è influenzata causalmente da due o più variabili. Le variabili causali che influenzano il collider non sono necessariamente associate. Il nome "collider" riflette il fatto che nei grafi causali, le punte delle frecce delle variabili che conducono al collisore sembrano "collidere" sul nodo che rappresenta il collider.[1]
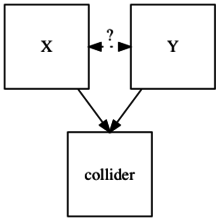
Il risultato di avere un collider in un percorso all'interno di un grafo causale è che il collider blocca l'associazione tra le variabili che lo influenzano.[2][3][4] Pertanto, il collider non genera una reale associazione incondizionata tra le variabili che lo determinano.
Il condizionamento sul collisore tramite analisi di regressione, stratificazione, progettazione dell'esperimento o selezione del campione in base ai valori del collider può creare un'associazione non causale tra X e Y (paradosso di Berkson). Nella terminologia dei grafi causali, il condizionamento sul collider apre il percorso tra X e Y. Questo può introdurre bias nella stima dell'associazione causale tra X e Y, introducendo potenzialmente associazioni dove non ce ne sono. Il condizionamento sui collider può quindi alterare grandemente i risultati dei test su teorie causali.
I collider a volte vengono confusi con le variabili confondenti. A differenza dei collider, le variabili confondenti dovrebbero essere controllate quando si stimano le associazioni causali, per lo stesso motivo per cui i collider invece non devono essere controllati.
Note
modifica- ^ Chapman & Hall/CRC monographs on statistics & applied probability, 2010, ISBN 978-1-4200-7616-5.
- ^ vol. 10, DOI:10.1097/00001648-199901000-00008, ISSN 1044-3983, OCLC 484244020, PMID 9888278, http://www.epidemiology.ch/history/PDF%20bg/Greenland,%20Pearl%20and%20Robins%201999%20causal%20diagrams%20for%20epidemiologic%20research.pdf.
- ^ Judea Pearl, Fusion, Propagation and Structuring in Belief Networks, in Artificial Intelligence, vol. 29, n. 3, 1986, pp. 241–288, DOI:10.1016/0004-3702(86)90072-x.
- ^ Judea Pearl, Probabilistic reasoning in intelligent systems: networks of plausible inference, Morgan Kaufmann, 1988.