Inconica
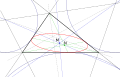
In geometria un'inconica è una conica che sia tangente ai tre lati di un triangolo o ai loro prolungamenti. Le inconiche di forma ellittica si chiamano inellissi. L'incerchio è caso particolare di inellisse.
Ogni inconica è descritta da un'equazione trilineare di tipo U2x2 + V2y2 + W2z2 − 2VWyz − 2WUzx − 2UVxy = 0 dove U, V, W sono funzioni delle lunghezze dei lati del triangolo e vengono chiamati parametri dell'inconica. Inoltre ogni equazione di tale forma descrive un'inconica. Nel caso di inconiche aperte (parabole ed iperboli), due dei tre punti di tangenza sono esterni al triangolo e posti lungo i prolungamenti dei lati.
Le tre rette che congiungono i vertici del triangolo con i punti di tangenza dell'inconica con il rispettivo lato opposto si intersecano in un solo punto chiamato punto di Brianchon. Le coordinate trilineari x:y:z del punto di Brianchon sono gli inversi dei parametri dell'inconica, ovvero 1/U:1/V:1/W.
Le coordinate trilineari dei tre punti di tangenza dell'inconica sono 0:W:V, W:0:U e V:U:0 mentre quelle del centro dell'inconica sono: cV + bW : aW + cU : bU + aV dove a, b, c sono le lunghezze dei tre lati del triangolo.
L'inconica è una parabola se e solo se bcU +acV + baW = 0. Il fuoco ha coordinate trilineari a/U2 : b/V2 : c/W2.