Solido di Steinmetz
In geometria solida, un solido di Steinmetz è un solido ottenuto come intersezione di due o tre cilindri aventi lo stesso raggio che si compenetrano perpendicolarmente.
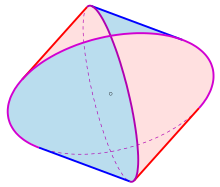
Il solido risultante dall'intersezione di due cilindri, che è topologicamente equivalente a un osoedro quadrato, è chiamato "bicilindro", mentre quello risultante dall'intersezione di tre cilindri è chiamato "tricilindro".
I solidi di Steinmetz sono così chiamati in onore del matematico Charles Proteus Steinmetz, che ricavò una formula atta a determinare il volume di tali intersezioni. Tuttavia il problema era già stato risolto in procedenza da Archimede, il noto matematico greco,[1][2] dall'antico matematico cinese Zu Chongzhi,[3] e, in tempi più recenti, da Piero della Francesca, noto matematico e pittore del Rinascimento italiano.[1]

Bicilindro
modificaIl volume di un bicilindro generato da due cilindri aventi raggio è dato dall'espressione
mentre l'espressione dell'area della sua superficie è:
Bisezionando un cilindro con un piano perpendicolare alle basi dei due cilindri dalla cui intersezione si genera il bicilindro, si ottiene un solido sulla cui forma è basato l'elemento architettonico chiamato volta a padiglione, ossia il caso quadrato di una volta a cupola, un solido a forma di cupola avente per base un qualunque poligono convesso le cui sezioni trasversali sono copie simili di tale poligono.
Dimostrazione dell'espressione del volume
modificaPer ottenere la formula del volume di un bicilindro è comodo considerarlo costituito da strati cuboidali quadrati di spessore infinitesimo (allo stesso modo per ricavare il volume della sfera si può considerare quest'ultima come costituita da innumerevoli dischi di spessore infinitesimo e raggio crescente man mano che si va dai poli al centro della sfera). Ciò porta all'espressione:
- .
È noto che i volumi di un cono retto, una semisfera e un cilindro aventi lo stesso raggio e la stessa altezza stanno tra loro in proporzione 1 : 2 : 3. Allo stesso modo si ha che i volumi di una piramide quadrata ( ), di un semi bicilindro ( ) e di un cubo ( ) aventi la stessa altezza e spigoli di base equivalenti è sempre 1 : 2 : 3.
Dimostrazione alternativa dell'espressione del volume
modificaSi considerino le equazioni dei cilindri orientati lungo l'asse x e l'asse y e aventi raggio :
Dalla figura si vede che il solido risultante dalla loro intersezione, ossia il bicilindro, può essere considerato composto da quattro biangoli, disposti simmetricamente attorno all'asse z. Per le equazioni cartesiane date sopra, il biangolo sito nei quadranti con x positivo può essere descritto dalle equazioni parametriche:
con e
Le altre tre parti possono essere descritte modificando parzialmente queste tre espressioni e/o passando da una all'altra a: e
Considerando ora la quarta parte di tale biangolo, ossia quella che si sviluppa nel quadrante con x, y e z positive e che in figura è rappresentata dalla superficie gialla, si vede che il volume sotteso da quest'ultima superficie sul dominio triangolare posto sul piano xy ed evidenziato in blu in figura è pari a un sedicesimo del volume dell'intero bicilindro. Quest'ultimo sarà quindi dato da:
Dimostrazione dell'espressione dell'area
modificaLa superficie considerata nel paragrafo precedente, ossia quella evidenziata in giallo, risulta utile anche per misurare l'area della superficie dell'intero bicilindro. Anche in questo caso, infatti, quest'ultima può essere ottenuta moltiplicando per 16 l'area di tale superficie , che è data dall'integrale della funzione nel già citato dominio triangolare:
Tricilindro
modificaIl risultato dell'intersezione di tre cilindri aventi assi perpendicolari è la superficie di un solido chiamato "tricilindro". Indicando con il raggio dei cilindri, tale solido è delimitato dalle equazioni:
La superficie è quindi costituita da 12 sezioni curve ed ha un totale di 14 vertici e 24 spigoli. In particolare su 6 dei 14 vertici incidono 4 spigoli, mentre sui restanti 8 ne incidono 3.
Per determinare il volume e l'area totale di un tricilindro con raggio , è possibile utilizzare la superficie evidenziata in azzurro nella figura a lato.
Volume
modificaUn tricilindro è costituito da un cubo interno di lato le cui facce combaciano con le basi di sei piramidi quadrate curve, la cui superficie laterale è composta da 8 sezioni come quelle evidenziate in azzurro in figura. Tale sezione si trova sopra un triangolo nel piano x con vertici in (0,0,0), ( ,0,0) e ( , ,0). La base di tale sezione si trova a un'altezza z = , mentre il suo vertice è a un'altezza . Il volume compreso tra la superficie azzurra e un piano posto a z= è quindi:
Considerando che il volume totale del tricilindro è dato dalla somma del volume del cubo sopraccitato e di 48 sezioni come quella sopra descritta, si ha:
Area della superficie
modificaLa superficie totale del tricilindro è pari a 24 volte l'area della sopraccitata sezione azzurra. Utilizzando un integrale di superficie come già precedentemente mostrato per il bicilindro, si può ricavale l'espressione dell'area della superficie totale del tricilindro:
Sia per il bicilindro che per il tricilindro, il rapporto tra area della superficie e volume è pari a , come nel caso di una sfera.
Più cilindri
modificaNel caso di intersezione di quattro cilindri di raggio , disposti in modo che i loro assi connettano i vertici di un tetraedro a punti corrispondenti al centro della faccia opposta, il solido risultante, avente 24 facce curve, ha un volume pari a:[4][5]
Nel caso di sei cilindri di raggio , disposti con gli assi paralleli alle diagonali delle facce di un cubo, il solido risultante, avente 36 facce curve, ha un volume pari a:[4][5]
Note
modifica- ^ a b Mark A. Peterson, The geometry of Piero della Francesca, in The Mathematical Intelligencer, vol. 19, n. 3, 1997, pp. 33-40, DOI:10.1007/BF03025346, MR 1475147.
- ^ Jan Hogendijk, The surface area of the bicylinder and Archimedes' Method, in Historia Mathematica, vol. 29, n. 2, 2002, pp. 199-203, DOI:10.1006/hmat.2002.2349, MR 1896975.
- ^ Frank J. Swetz, The volume of a sphere: A Chinese derivation, in The Mathematics Teacher, vol. 88, n. 2, Febbraio 1995, pp. 142-145, JSTOR 27969235.
- ^ a b c (EN) Eric W. Weisstein, Solido di Steinmetz, in MathWorld, Wolfram Research. URL consultato il 2 agosto 2021.
- ^ a b c M. Moore, Symmetrical intersections of right circular cylinders, in The Mathematical Gazette, vol. 58, n. 405, 1974, pp. 181-185, DOI:10.2307/3615957, JSTOR 3615957.
Altri progetti
modifica- Wikimedia Commons contiene immagini o altri file su Solido di Steinmetz
Collegamenti esterni
modifica- (EN) Eric W. Weisstein, Solido di Steinmetz, su MathWorld, Wolfram Research.